Indijska matematika

Indija nam je dala prirodan način prikazivanja bilo kojeg broja pomoću samo deset znakova… Ovo je dubokoumna i važna ideja koja nam se danas čini tako jednostavnom da često zaboravljamo njenu pravu vrijednost. Veličinu ovog otkrića moramo cijeniti tim više kad se uzme u obzir da je ono promaklo takvim umovima kao što su Arhimed i Apolonije – Pierre Simon Laplace, francuski matematičar i astronom…

Indija je od drevnih vremena pa sve do danas domovina vrsnih matematičara. U dalekim ved­skim vremenima matematika je bila tijesno povezana s religijom, jer je prvenstveno služila u ceremonijalne svrhe – za točno određivanje početaka ceremonija kroz astronomske proračune te za izradu žrtvenika. Staroindijski matematičari bili su prvenstveno astronomi (astrolozi) i svećenici, a svoja su znanja iznosili u stihovima, u tzv. sutrama.

Osnovna razlika između indijske i grčke matematike jest u tome što su Grci bili više orijentirani na geo­metriju a Indijci na aritmetiku. Za Indijce je geometrija imala isključivo uporabnu vrijednost, dok su Grci geometriju razvijali kao teoretsku disciplinu koju su koristili za dokazivanje svojih poučaka. S druge strane, Indijci su razvili besprijekoran numerički sustav te utemeljili i razvili algebru koju će od njih preuzeti Arapi i prenijeti dalje Europi te tako otvoriti put modernoj ­matematici.

Povijesno se indijska matematika može podijeliti na pet velikih cjelina, upitnog vremenskog datiranja:

1. drevna vremena (vedski period):

a) rani vedski period (barem 6000. pr.Kr. – 1000. pr.Kr.)

b) kasni vedski period (1000. pr.Kr. – 500. pr.Kr.)

2. pretklasični period (500. pr.Kr. – 400.)

3. klasični period ili Zlatno doba (400. – 1200.)

4. kasni klasični period (1200. – 1800.)

5. moderno doba (nakon 1800.)

Vede su najstariji indijski sveti tekstovi u kojima su sačuvana znanja iz različitih područja: religije, medicine, astronomije, matematike, itd. Metode računanja kojima se služila vedska matematika bile su jednostavne i praktične tako da su upotrebljive i za računanje napamet.

U kasnim vedskim Śulba sutrama matematika se razvija zbog potreba rješavanja praktičnih geometrijskih problema (uglavnom vezanih uz konstrukciju ceremonijalnih žrtvenika). Iz tih vremena poznat je cijeli niz tzv. Pitagorinih trojki brojeva, tj. prirodnih brojeva koji zadovoljavaju Pitagorin poučak:
a2 + b2 = c2 a to je dovelo do uvođenja iracionalnih brojeva. Razvili su metodu vađenja drugog korijena preko rekurzivnih formula.

Đainistički matematičari pretklasičnog perioda najviše se spominju kao važna spona između matematičara vedskog perioda i onih iz klasičnog perioda. Njihov je povijesni značaj u tome što su indijsku matematiku odvojili od njene religijske i obredne primjene. Oni u matematiku uvode i pojam beskonačnosti.

Smatra se da su prvi upotrijebili riječ shunya (praznina) kao izraz za nulu. Za razliku od Grčke, Indija je prazninu (nulu) i beskonačnost prihvatila bez straha.

Zlatno doba

Svoj vrhunac indijska matematika doseže u klasičnom periodu. U vrijeme kad Europa sve više tone u mrak, a Arapi još nisu preuzeli baklju matematičkog znanja, u Indiji cvjeta znanost. Tijekom ovog perioda pojavila se čitava plejada genijalnih matematičara koji su proširili znanja iz geometrije i trigonometrije, postavili temelje današnjeg brojevnog sustava i utemeljili alge­bru. Spomenimo samo najpoznatije: Aryabhata I., Varahamihira, Brahmagupta, Bhaskara I., Mahavira, Bhaskara II. Njihov se utjecaj s vremenom proširio i izvan granica Indije te konačno stigao i do Europe.

Aryabhata I.

Prvi u nizu, i jedan od najvećih, svakako je Aryabhata I. iz Kusu­mapure (476.–550.). Njemu se pri­pisuje zasluga da je matematiku ustanovio kao samostalnu disci­plinu, odvajajući je od njene religij­ske funkcije.
Njegovo je najpoznatije djelo Aryabhatiya, matematičko-astronomska rasprava u kojoj je sakupio astronomska i matematička znanja starih Indijaca i Grka, dodajući tome i cijeli niz vlastitih otkrića. Uz astronomiju, planarnu i sfernu trigonometriju te aritmetiku, u ovoj raspravi nalazimo i prve početke algebre.

Rasprava je napisana u stihovima u izuzetno sažetom obliku, tako da je često teško shvatiti njihov pravi smisao. Srećom, Aryabhatin učenik Bhaskara I. kasnije je dodao detaljne komentare.

U drevnoj Indiji, sve do otprilike 500. g. pr.Kr., svi su se tekstovi prenosili isključivo usmeno, pa su radi lakšeg pamćenja sva znanja, pa tako i matematička, bila iznesena u stihovima.

Učenici su najprije napamet učili matematičke probleme i pravila sažeto zapisane u stihovima, a nakon toga su prelazili na proučavanje proznih komentara koji su s puno više detalja objašnjavali probleme. Ipak, prozni dio je bio manje cijenjen od onog u stihu u kojem se iznosila sama ideja.

Aryabhatiya se sastoji od sto osam strofa podijeljenih u četiri poglavlja ili pade:

1. Gitikapada – sadrži astronomske tablice, velike vremenske jedinice te, u jednoj strofi, tablice za trigonometrijsku funkciju sinus.

2. Ganitapada (matematika) – objašnjava različite geometrijske i aritmetičke formule, te linearne, kvadratne i diofantske jednadžbe.

3. Kalakriyapada (vremenski izračuni) – stihovi o astronomskim pojmovima i veličinama

4. Golapada (san. gola – kugla, sfera) – govori o geometrijskim i trigonometrijskim aspektima nebe­ske sfere, o različitim pravilima vezanim uz trigonometrijske probleme te o obliku Zemlje i pojavama u Sunčevom sustavu i zviježđima ­zodijaka.

Iako su tvrdnje u Aryabhatiyi navedene bez dokaza, odnosno izvoda, suvremeni matematičari smatraju da to ne znači da ih autor nije znao dokazati, nego da je tada to bila uobičajena forma izlaganja.
Od vremena Bhaskare I. (VII. st.) prozni su komentari sve češće sadržavali i upapatti – neku vrstu dokaza.

Bhaskarini komentari Arya­bhatiye su imali sljedeći oblik: Najprije bi u stihu naveo neko pravilo ili problem, a zatim ga komentirao u nekoliko koraka:

• pojašnjenje pravila (izvodi su u to doba još rijetki, ali se kasnije sve češće koriste)
• primjer (uddesaka), najčešće u stihovima
• postavka (nyasa/sthapana) numeričkih podataka
• izrada (karana) rješenja
• provjera, verifikacija (pratyayakarana) odgovora. Ovaj je dio u XIII. st. izbačen jer su izvodi postali uobičajeni.

Utjecaj Aryabhatiye na indijske matematičare usporediv je s utjecajem Euklidovih Elemenata na zapadnu matematiku.

Kao i većina matematičara drevne Indije, Aryabhata je u prvom redu bio astronom. Glavnina njegovih matematičkih otkrića proizlazi iz astronomskih proučavanja. Kompleksni proračuni u kojima se pojavljuje više varijabli prisilili su Aryabhatu da potraži način kako pojednostavniti astronomske proračune. Tako je prvi put zaista upotrijebljena algebra umjesto uobičajene aritmetike.

Matematika se na sanskrtu naziva ganita. Algebarske forme računanja dobile su ime bijaganita što znači “druga matematika”, zato što je ovaj način računanja smatran paralelnim onom uobičajenom i dotad jedinom načinu.
Kao primjer Aryabhatinog pra­vila navest ćemo njegov postupak za računanje površine trokuta. U 6. sutri Ganitapade piše:

Promatramo li trokut, umnožak okomice i polovine stranice daje površinu.

U našem sustavu označavanja to bi značilo: P = va ∙ a/2

Izuzetno je zanimljivo da je vrijednost broja π poznavao točno na četiri decimale (π ≈ 3,1416) što je najbolja aproksimacija do pojave moderne matematike
(π = 3,14159265358979… ):

Dodaj četiri stotini, pomnoži s osam i dodaj šezdeset dvije tisuće. Rezultat je približno jednak opsegu kružnice promjera dvadeset tisuća. Na ovaj je način dat odnos opsega i promjera.

Drugim riječima:
π ≈ ((4+100)·8+62000)/20000
= 62832/20000 = 3,1416

Uz naziv Bhaskarinog djela Lilavati postoji jedna legenda:

Kad se Bhaskari rodila kći Lilavati, astrolozi su prorekli da joj nije suđen brak. Bhaskara se s time nije htio pomiriti te je upotrijebio sve svoje znanje astrologije i izračunao da postoji samo jedan jedini dan i jedan jedini trenutak u tom danu kad se ona može sretno udati. Samo tada i nikada više.

I kad je došao taj sretan dan, mladoženja i uzvanici okupili su se na obredu vjenčanja, a Bhaskara i njegova obitelj pomno su gledali na vodeni sat koji je trebao pokazati kad će nastupiti taj jedini povoljan trenutak za udaju.

Međutim, dok se naginjala nad satom, uzbuđena mladenka nije primijetila da je s njene ogrlice otpao biser i pao u vodeni sat. Biser je usporio protjecanje vode, a da to nitko nije opazio. I, premda je vjenčanje dalje teklo prema planu, nitko nije bio svjestan da je onaj jedini povoljan trenutak nepovratno prošao. Lilavati nije mogla izbjeći prorečenu sudbinu – njen muž je umro ubrzo nakon vjenčanja.

Kako bi utješio kći koja je ostala udovica do kraja života, Bhaskara je obećao da će prema njoj nazvati svoju knjigu koja će trajati za sva vremena, i rekao joj je: Dobro ime je drugi život i temelj vječnog postojanja.

Tako je djelo Lilavati dobilo ime.

I, štoviše, naglasio je da se radi o aproksimaciji, a ne točnoj vrijednosti. Bio je svjestan da je broj π iracionalan broj (tj. da se ne može zapisati u obliku razlomka).

Vjerojatno najveći doprinos matematici Aryabhata je dao u rješavanju diofantskih jednadžbi (jednadžbi s cjelobrojnim rješenjima). Ove su jednadžbe važne za izračunavanje različitih astronomskih ciklusa. Za te je potrebe izmislio tzv. kuttaka algoritam, tj. algoritam usitnjavanja, pretvaranja u prašinu. Metoda se sastoji u postupnom smanjivanju koeficijenta u jednadžbi. I danas se ovaj algoritam često spominje kao Aryabhatin algoritam.

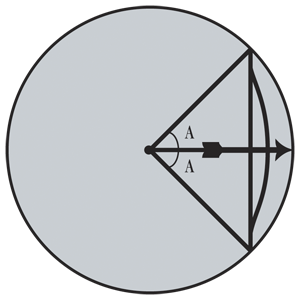
Bhaskarin dokaz Pitagorinog poučka

Aryabhata prvi daje i definiciju trigonometrijske funkcije sinus.

Ne definira je na naš način, kao omjer nasuprotne katete i hipotenuze, nego kao duljinu polutetive.

Kružnicu je podijelio na 21600 dijelova, tj. onoliko dijelova koliko iznosi puni kut izražen u minutama (360° × 60 = 21600’), i taj dio koristi kao mjeru.

Zanimljiv je put kojim je nastao naziv sinus. Sanskrtska riječ jya-ardha koju je Aryabhata koristio za sinus znači “polutetiva” a često se skraćeno izgovarala jya.

U arapski je svijet ova riječ ušla kao jiba a kako se u arapskom samoglasnici ne pišu nego dodaju prilikom čitanja, ovo se pisalo kao jb a s vremenom čitalo jiab što znači zaljev, uvala ili nabor na odjeći, jer jiba na arapskom nije imalo značenja.

Gerard Kremonski je, prevodeći ove tekstove na latinski, ovu riječ preveo sa sinus, tj. zavoj ili nabor.

Brahmagupta

U VII. stoljeću u Ujjainu djeluje drugi velikan indijske matematike, Brahmagupta. On je napisao četiri astronomsko-matematička teksta od kojih je najpoznatiji Brāhmasphutasiddhānta (Isprav­no zasnovano učenje Brahme).
Ova se knjiga sastoji od dvadeset pet poglavlja u kojima se uz astronomiju pojavljuju teoremi iz algebre, aritmetike i geometrije.

U dvanaestom poglavlju postavio je svoj poznati teorem o dijagonalama tetivnog četverokuta (četverokuta upisanog u kružnicu) i formulu za njegovu površinu kad su poznate duljine stranica.

Ta formula je poopćenje poznate Heronove formule za površinu trokuta.

U osamnaestom je poglavlju dao i formulu za jedno rješenje kvadratne jednadžbe zapisane u obliku: ax2 + bx = c.

Brahmaguptino poimanje bro­jevnog sustava bilo je ispred njegova vremena. Razvio je pozicijski sustav zapisivanja brojeva. Uveo je moderni koncept nule tako što ju je definirao kao rezultat oduzimanja broja od sebe samog. Time je ona stekla ravnopravan status s drugim brojevima, status koji će u Europi steći tek u XVII. st. Također je uveo računske operacije s negativnim brojevima.

Bhaskara II.

Bhaskara ili Bhasakracharya (san. acharya – učeni) je posljednji veliki matematičar Zlatnog doba i možda najveći indijski matematičar svih vremena. Njegovo je glavno djelo Siddhāntaśiromati (Krun­ski dragulj ispravnosti), napisano oko 1150. g., a sastoji se od četiri ­dijela:
1. Lilavati (aritmetika)
2. Bijaganita (algebra)
3. Goladhyaya (sferna geometrija)
4. Grahaganita (astronomski
proračuni)

Pisao je u stihovima, ali je dodavao i objašnjenja u prozi. U njima je sistematizirao znanja svojih prethodnika, iznio dokaze mnogih teorema koje su oni izrekli te dao vlastiti nemjerljiv doprinos u svim područjima.

Popunio je mnoge praznine u Brahmaguptinom djelu. Sustavno je izložio decimalni (pozicijski) način zapisivanja brojeva. Između ostalog, otkrio je da kvadratna jednadžba ima dva rješenja, dokazao je da broj podijeljen s nulom daje beskonačnost, dao je geometrijski dokaz Pitagorinog poučka a postavio je i temelje diferencijalnog i integralnog računa davno prije Newtona i Leibnitza.

U današnje vrijeme indijski mate­matičari nastavljaju stopama svo­jih slavnih prethodnika. Indiji se odaje sve veće priznanje za velika posti­gnuća na području ove znano­sti. Najpoznatiji je predstavnik moder­nog doba svakako bio Srinivasa Ramanujan (1887.–1920.), ali ne treba zaboraviti ni Harish-Chan­dru (1923.–1983.) te Manjula Bhargavu (1974.). Priznanje Indiji za njen doprinos iskazano je i time što je Međunarodni kongres matematičara 2010. godine održan u Hyderabadu u Indiji.

Vesna Perhat